For a while I've been tinkering with animated looping GIFs. Inspired by Dave "beesandbombs", I started making them using Javascript and HTML5 canvas when I realized that I could write a crude editor by reusing some code I originally wrote for Forgecore.

It was an interesting activity, along the theme of making beautiful things out of coding.

A very recurrent subject in the animations I've made is the golden ratio. It fascinates me and that's pretty common, it begun fascinating people very long time ago. What I find particularly striking the strong contrast between how people can perceive it: its recurrence in nature can be seen as some sort of God's signature or as the proof that evolution really works because species that arranged their structures according to the most irrational of number managed to thrive.

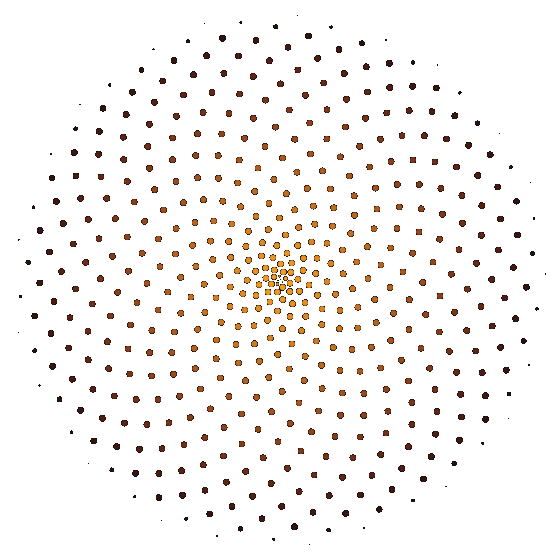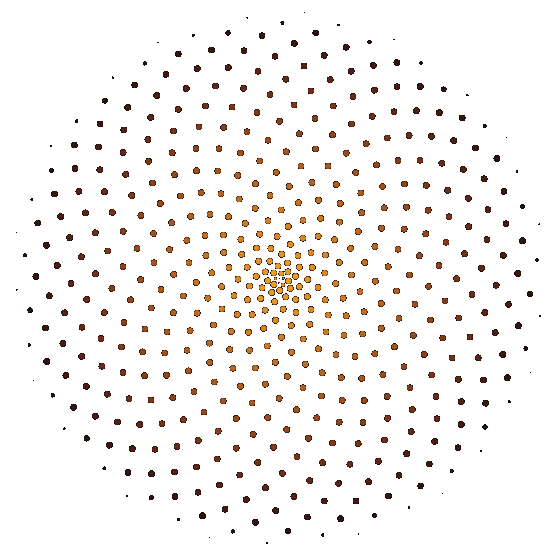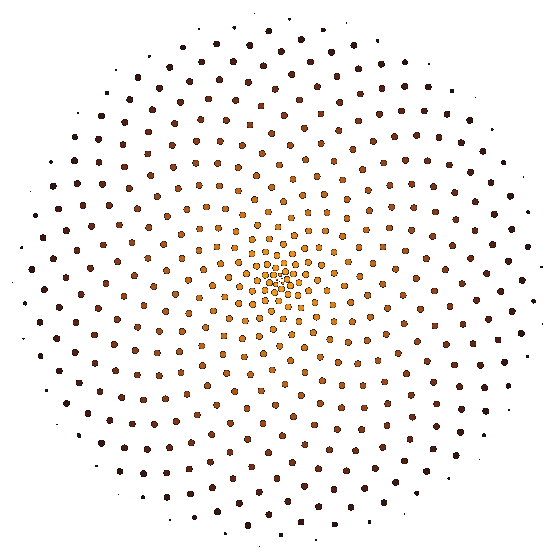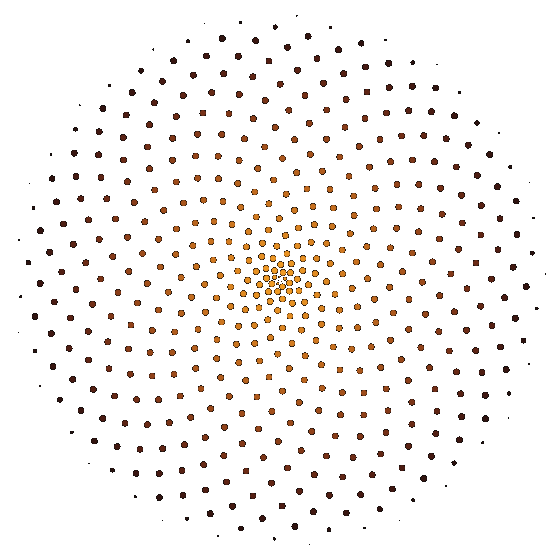
After watching this video by Numberphile on the subject, I started experimenting with an animation loop of a blooming flower.

The disposition of the petals follows the golden ratio, which is approximately 1.618033. Being around a circle, we can consider only the decimal part as the 1 would be a complete turn. So each petal is 0.618033 of a turn apart of his neighbors.

To make the animation loop seamlessly, I had to make petals grow so that at the end of the loop they would be in the same position and have the same shape of some other petal. In my first attempt I tried to make each petal grow and move to the position of the next one, but it was a mess: the duration of the loop must be as short as possible to avoid increasing too much the file size and the whole flower would make that 0.618033 of a turn... it was spinning like crazy.

We are talking about spinning in circles anyway, so I figured out that if each petal grows to end up on the second after it would rotate by 0.618033 x 2 = 1.236066 of a turn but I could rotate the whole image of one turn in the opposite direction, so that the image would appear to rotate of just 0.236066 of a turn.

It doesn't work with the third after anyway, as 0.618033 x 3 = 1.854099 and it will make things worse.

I have to be honest, I didn't analyze the problem properly at all. I guess I'm too much of a programmer and too little of a mathematician. I did what a real code monkey would do: get the solution by brute force. I couldn't grow too much each petal on a loop or the animation would get messy anyway, so I've opened the browser's console and I've tried to find what was the lowest number that multiplied by the golden ratio gives a value near to an integer:

var list = [];

for(var i = 1; i < 100; i++) {
    list.push({ i: i, val: (0.618033 * i) % 1 })
}

list.sort(function(a, b) {
    if(a.val < b.val) return -1;
    else return 1;
})

console.log(list);

And the results were these, a bit tainted by Javascript's lack of precision on float values:

[{
    i: 89,
    val: 0.004937000000005298
}, {
    i: 34,
    val: 0.013122000000002743
}, {
    i: 68,
    val: 0.026244000000005485
}, {
    i: 13,
    val: 0.03442900000000115
}, {
    i: 47,
    val: 0.04755100000000212
}, { ...

I discarded 89 because it's too big, so there it is, my "magic" number: 34.

I published the GIF on Twitter and Numberphile retweeted it, so it got a bit of visibility. Someone asked about how it was made and I've explained briefly the "34" story. At that point a seemingly innocent tweet unleashed an "EUREKA!" moment in me, followed by the bitter aftertaste of realizing how sometimes I'm a chimp whacking hands on a keyboard.

So yeah, what I was looking for were Fibonacci numbers. The ratio of two consecutive Fibonacci numbers tends to the golden ratio, in other words they are integers that multiplied by the golden ratio give a result approximated by an integer.

Some Fibonacci numbers don't appear in the result of my code because the modulo operation I've used doesn't consider numbers that are good approximations by a negative amount. For example, the modulo of 55 x 0.618033 will give 0.991815 and be pushed to the very end of the list, while it can be considered as -0.008185 and be placed between 34 and 89, right where it belongs.

A phrase I've heard a lot when talking about game development is: "If you can fake it - fake it". If the target is to release something that plays well, it may be a valid point because it hasn't to be necessarily accurate or realistic. But I can't stop thinking of how much learning is left behind by following this principle.